Anomalous transport | Katherine I. Driscoll

Uncovering the mechanism underlying anomalous electronic transport is one of the main challenges facing the condensed matter physics community today. Generally speaking, anomalous (or “bad”) metals are classified as those whose resistivity exceeds the Mott-Ioffe-Regel (MIR) limit as the temperature increases. This limit arises from a description of electron transport that is based upon scattering and the limiting resistivity is calculated as that achieved when one considers the shortest allowable scattering length. This minimal scattering length is typically considered to be the lattice spacing for any given system.

So-called bad metals exceed the MIR limit as a function of temperature, while the resistivity of conventional metals saturate at, or before, this limiting value.

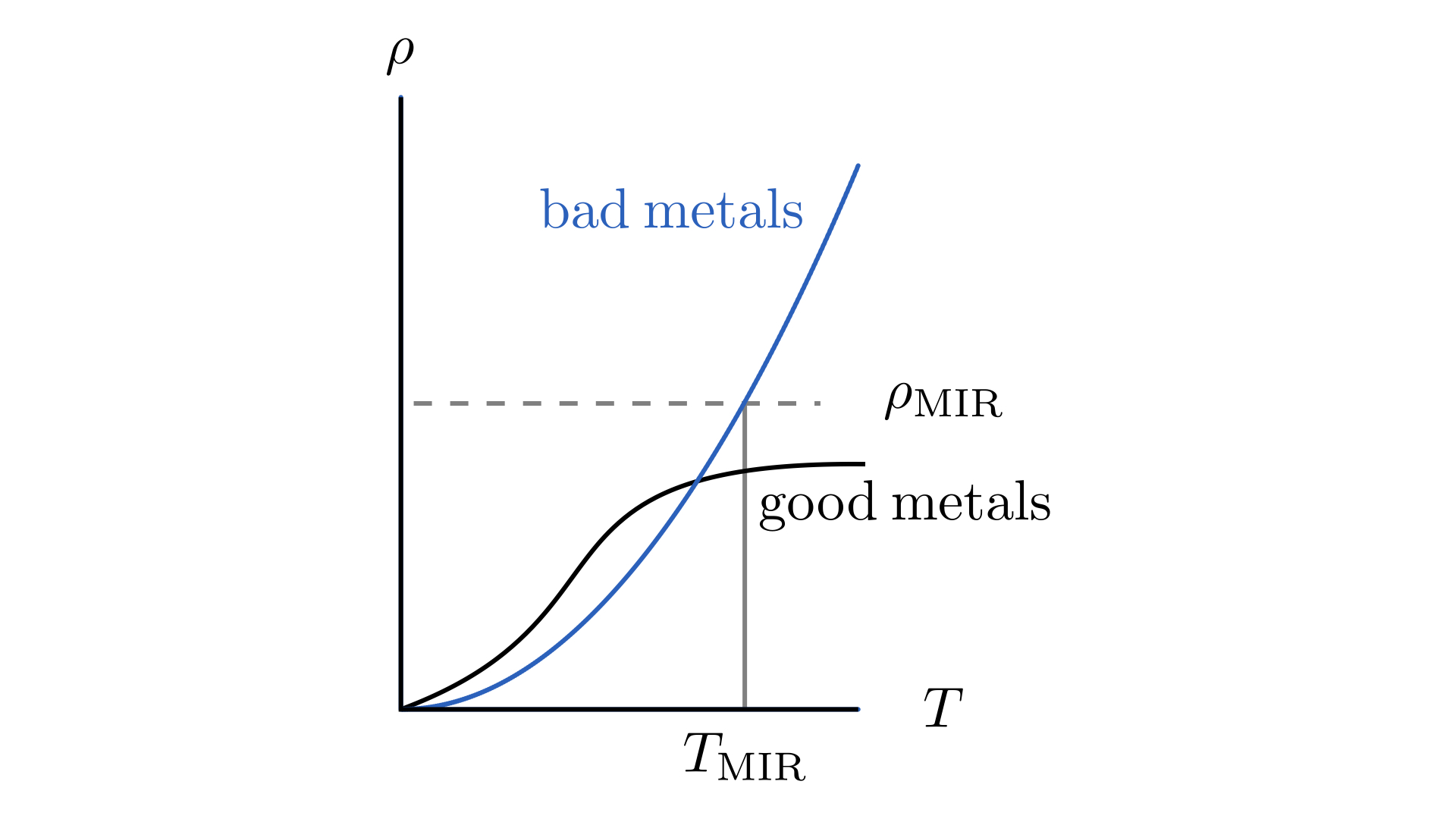
In the standard Drude model of conductivity, the resistivity is calculated as the inverse of the DC conductivity value, \(\rho = 1/\sigma_{DC}\). When disorder is added to a system, the scattering rate tends to increase which means that the DC conductivity value decreases, thereby increasing the resistivity. This increase typically does not exceed the MIR limit. However, when a system has disorder and strong quantum interferences, then Anderson localization can occur in which the electrons are unable to move, or to transport. This localization phenomenon causes the DC value to drop to zero, thereby leading to infinite resistivity.

Between the standard picture of Drude conductivity and the extreme case of Anderson localization, there ought to lie another picture of electron transport–one in which the electrons are almost localized. In this picture, the DC value would be smaller than expected in the conventional Drude framework, but still non-zero. This reduction in the DC value could provide a plausible mechanism to explain anomalous resistivity patterns observed in various bad metallic systems.

Illustration of the three regimes of electrical conduction: conventional Drude transport (black), Anderson localization (green), and the proposed "almost-localized" transport (blue).

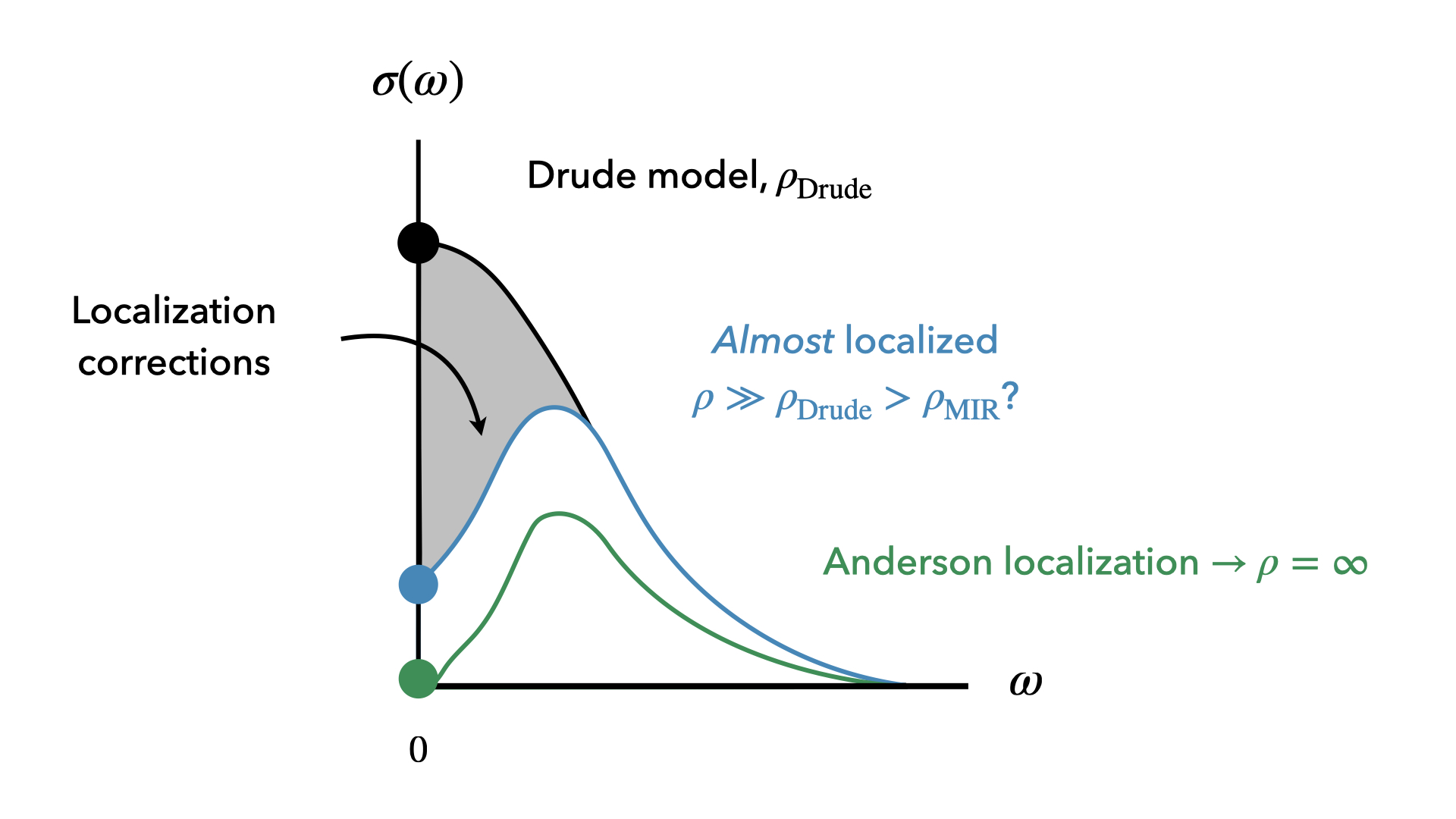
Indeed, the decrease of the DC value of the conductivity could lead to the development of a displaced Drude peak, another signature of anomalous metallic transport. Interestingly, this displaced Drude peak, or DDP, is not observed in all bad metals and has escaped a theoretical understanding thus far.

In order to examine the effect of long-range interactions on electron transport, we established a project using classical Monte Carlo simulations. The use of a classical technique is justified by the long timescales necessary for collective charge rearrangement, as discovered in our previous project at zero temperature. This technique enables us to study much larger system sizes than in our previous exact diagonalization study. We also updated our long-range interacting model to include on-site interactions, or the \(U\) term from the Hubbard model.

\begin{equation} H = -t \sum_{\langle ij \rangle, \sigma} \big( \hat{c}^{\dagger}_{i\sigma} \hat{c}_{j\sigma}^{} + h.c. \big) + \frac{V}{2} \sum_{ij} \frac{ ( \hat{n}_{i} - \bar{n} )( \hat{n}_{j} - \bar{n} ) }{ R_{ij} } + U \sum_{i} \hat{n}_{i,\uparrow} \hat{n}_{i,\downarrow} \end{equation}

The classical Monte Carlo calculations treats the above Hamiltonian to the lowest order in \(t\), as discussed in works by Mousatov, Esterlis, and Hartnoll. While this level of treatment is already capable of displaying anomalous transport in the form of extremely high resistivity values, it is unable to provide a microscopic explanation for DDPs.

To further explore the effect of long-range interactions, we developed a mixed quantum-classical method that treats the collective charge environment classically while accounting for the quantum fluctuations for inidividual electron motion. The collective charge environments are sampled via Monte Carlo calculations. At each Monte Carlo timestep, we build a one-body Hamiltonian to describe electron motion in the fixed charge environment. This method necessarily relies on the fact that individual electron motion occurs on a much more rapid timescale than global rearrangements.

Our mixed quantum-classical method indeed produces DDPs in the optical conductivity spectra when localization corrections are properly treated, as described in Fratini and Ciuchi.

DDPs arise in the optical conductivity spectra at low frequencies when localization corrections have been applied to our mixed quantum-classical method (left). The inset provides a zoomed in perspective of the DDPs. These DDPs result in high values of the resistivity (right). Resistivity values from the semi-classical method (green) and our mixed quantum-classical scheme (light blue) are compared to typical values (dark blue) from the cuprate family of superconductors, a well-known strongly correlated and bad metallic system. The MIR limit is plotted in black.

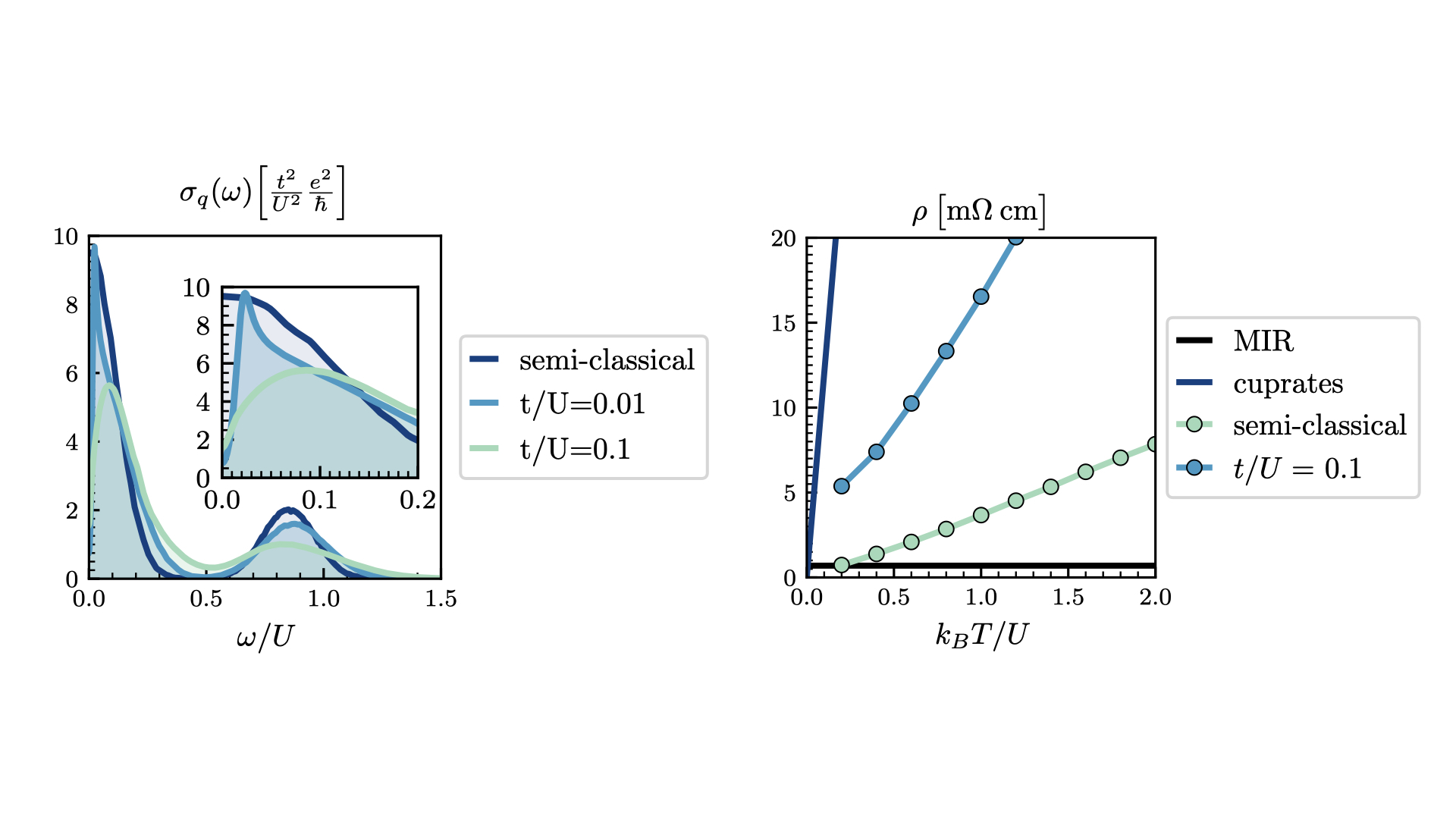
These calculations from our mixed quantum-classical method establish as a proof-of-principle that the disorder arising from long-range interactions can lead to DDPs and anomalous values of resistivity. Of course, these calculations cannot fully explain all of the scattering behavior in specific materials, such as the cuprates. Nonetheless, these calculations serve as an important first step towards providing a plausible microscopic explanation of anomalous electron transport.

The natural next step is to properly treat the quantum effects by means of the finite temperature Lanczos method, a technique that is currently under development. While this method serves as a natural extension of our exact diagonalization work at zero temperature, it will limit the accessible sizes and careful benchmarking must be performed in order to rule out any finite-size effects.